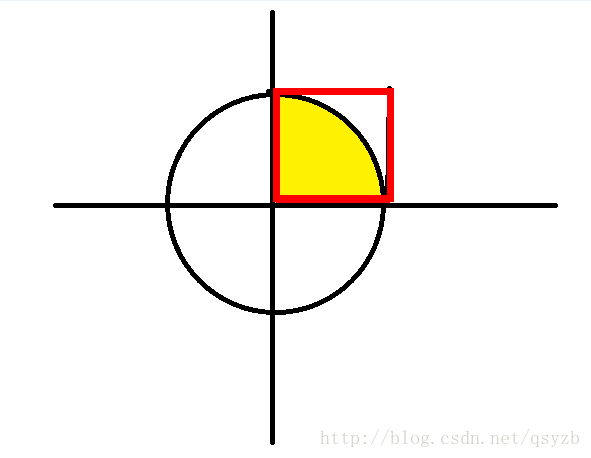
蒙特卡洛算法是一个基于几何概率模型的近似估计真实值的方法，可以近似估计出圆周率π和一些被积函数比较复杂不容易求出积分的积分值。

近似估计出圆周率π举例：

假设在正方形内投掷随机点数量为N(N∈N*)，则按几何概率，当N很大时，落在圆中数量为n(n∈N*), 而N与n的比值等价于两者的面积比，即：

πr²/4r²= n/N

=>  π = 4n/N

C++代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <iostream>
#include <random>
#include <cmath>
 
const double r = 2;
 
double Random(int min, int max);
 
class location {
public:
	double x, y;
 
	location(double x, double y) {
		this->x = x;
		this->y = y;
	}
	location() {
		this->x = Random(0, 2 * r);
		this->y = Random(0, 2 * r);
	}
};
 
// 随机[min,max]
double Random(int min, int max) {
	// 生成[0,1]
	double random_number = (double)std::rand() / RAND_MAX;
 
	// 生成一个整数部分范围为 [min,max-1] 的随机数。
	int integer_part = std::rand() % max;
 
	// 将整数部分与随机数的小数部分相加。
	double result = static_cast<double>(integer_part) + random_number;
 
	return result;
}
 
double GetPai(int N) {
	location center(r, r);
	int n = 0;
 
	for(size_t i = 0; i < N; i++) {
		location happen;
		bool ifCircle = pow((happen.x - center.x), 2) + pow((happen.y - center.y), 2) <= pow(r, 2);
		ifCircle&& n++;
	}
	double Pai = (double)4 * n / N;
 
	return Pai;
}
int main() {
	int N;
	while(true) {
		std::cout << "请输入蒙特卡洛试验次数：" << std::endl;
		std::cin >> N;
		double pai = GetPai(N);
		std::cout << "PAI计算结果为：" << std::endl << pai;
		std::cout << Random(1, 10)<<std::endl;
	}
}

运行结果：